|
|
CORSO DI RILIEVO DELLíARCHITETTURA
Docente Dott. Arch. Francesco Maglioccola
PROCEDURE DI RILEVAMENTOParte quarta
Dispensa ad uso degli studenti del corso di Diploma Universitario in Edilizia
|
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
| Indice degli argomenti affrontati durante le lezioni |
Il prelievo dei dati
Parte quarta Precedente - Successiva
|
|||||||||||||||||||||||||
| PROCEDURE DI RILEVAMENTO
|
||||||||||||||||||||||||||
| Il prelievo dei dati | ||||||||||||||||||||||||||
| Osservare per apprezzare il valore metrico degli oggetti attraverso la percezione visiva. Occhio fisso e non in movimento. Campo visivo. Proporzione con oggetti posti ad una certa distanza. | Un modo per assegnare delle misure ad un manufatto architettonico
è quello che prevede la comparazione delle sue parti con elementi
ad esso esterno, o tra gli stessi elementi. Nel primo caso si utilizzano
strumenti che permettono di relazionare un elemento di misura nota con
uno di cui si vuol conoscere il valore metrico. Un modo molto semplice,
ma abbastanza grossolano, di pervenire ad un valore è quello che
prevede l'uso esclusivo dell'occhio. Tenendo teso un braccio e rapportando
la dimensione del proprio dito all'elemento che si vuol misurare, facendo
una piccola proporzione tra la grandezza ad esempio della finestra ed il
proprio dito, conoscendo la distanza dal punto in cui siamo al punto cui
si riferisce la dimensione ignota, ricaviamo proporzionalmente il valore
della finestra.
L'occhio è anche in grado di percepire con buona approssimazione una forma quadrata, per cui si riesce a costruire virtualmente sul disegno della facciata un quadrato riportando in alzato delle grandezze prese sul piano orizzontale. Assegnando dei valori metrici probabili alle forme architettoniche si perviene alla definizione dei manufatti nelle loro entità metriche. Ad esempio se si rileva un'architettura contemporanea, si può utilizzare quale parametro l'altezza dell'interpiano che si aggira intorno ai tre metri, per cui, proporzionalmente si assegneranno i valori alle varie aperture. Ancora, si può utilizzare come elemento di raffronto l'altezza della ringhiera, assegnata pari al valore di un metro. |
|||||||||||||||||||||||||
| Il dimensionamento degli elementi architettonici: | Unità di misura: sistema metrico decimale, sistema
anglosassone (inglese: pollici, piedi).
Per misura si intende non solo l'insieme dei dati dimensionali, ma in generale dei dati qualitativi. Nel dimensionamento degli elementi architettonici vi é il problema della valutazione quantitativa. I parametri e lemodalità applicative di tale valutazione possono essere riassunte nei seguenti punti: 1 Rapporto tra architettura e proporzione 2 Rapporto tra orgnismo umano e organismo architettonico 3 La misurazione in palmi, piedi parigini, metri ecc. (metrologia) - Rif. regole dei cinque ordini di Giacomo Barozzi detto il Vignola. |
|||||||||||||||||||||||||

|
||||||||||||||||||||||||||
| Fattori di conversione per le lunghezze tra il Sistema internazionale ed il sistema anglosassone |
|
|||||||||||||||||||||||||
| Il prelievo dei dati dalle rappresentazioni | La tipologia di informazioni che si possono derivare
dalle rappresentazioni variano a seconda del tipo di rappresentazione (assonometria,
pianta, sezione, prospettiva, ecc.) e dei tematismi affrontati - carte
tematiche - alle quali ad esempio appartengono le carte catastali. Non
si possono prelevare elementi da rappresentazioni che non si pongono come
finalità la loro valutazione. Ad esempio volendo analizzare un estratto
di mappa catastale del NCEU conservata presso líUTE, alla scala 1/2000
non sarà probante la configurazione geometrica della particella,
ed avrà maggior valore il dato numerico che riporta líestensione
del lotto piuttosto che la misurazione che si possa fare sulla mappa.
|
|||||||||||||||||||||||||
| Il prelievo dei dati dalle mappe - Immagini bidimensionali cartacee | Supponiamo di dover prelevare dei dati metrici da una
rappresentazione grafica cartacea di un manufatto architettonico. Se nostro
interesse è solo la morfologia dell'oggetto possiamo attuare semplicemente
una lettura dei rapporti proporzionali esistenti tra le singole parti.
Questa operazione è indipendente dalla scala di riduzione delle
misure. Se invece vogliamo prelevare delle informazioni metriche è
necessario conoscere la scala di riduzione del grafico. Se questa è
indicata in calce al disegno semplicemente con una scritta del tipo ìscala
1:50î non ci garantisce sul fatto che il grafico non abbia subito delle
riduzioni o ingrandimenti, per questo dovremmo avere segnalata líinformazione
metrica su almeno una lunghezza in maniera da verificare la correttezza
della indicazione didascalica.
|
|||||||||||||||||||||||||
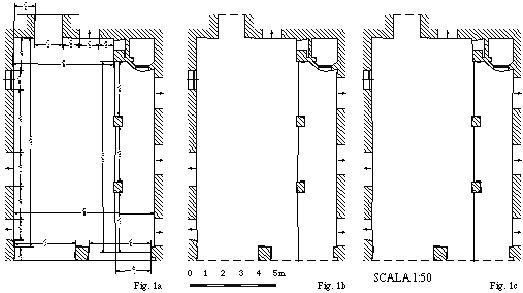
| Fig. 1a - Pianta
quotata senza alcuna indicazione in merito alla scala di riduzione.
Fig. 1b - Pianta con l'indicazione di una scala grafica. Fig. 1c - Pianta con l'indicazione di una scala numerica. |
|
|||||||||||||||||||||||||
| Laddove manca qualsiasi tipo di informazione circa la
scala di riduzione vi sono dei casi particolari nei quali possiamo ricavare
con una certa approssimazione líunità di misura sul grafico rispetto
a quella reale rapportando alcuni segni riconoscibili dei quali possiamo
ipotizzare il loro valore di misura. Ad esempio, se ci si trova di fronte
alla rappresentazione di un edificio per civile abitazione contemporaneo,
e ritroviamo rappresentata in pianta una scala, sapendo che i canoni progettuali
indicano in 30 cm c.a. il valore ottimale per la pedata di una rampa, si
può ritrovare la scala del disegno facendo riferimento a quella
misura. L'errore che si commette nel prelevare informazioni metriche dalle
rappresentazioni cartacee è direttamente proporzionale alla
scala di riduzione del grafico ed è funzione dell'uso del valore
metrico da individuare.
|
||||||||||||||||||||||||||
| Con líuso di un righello | Supponiamo di voler misurare la grandezza di un ambiente
rappresentato in pianta in cui è riportata il valore del rapporto
di scala indicato in calce al disegno. Una prima procedura è quella
che vede líutilizzo di un righello o di uno scalimetro. Con un righello
si legge il valore di lunghezza di un segmento sul disegno corrispondente
ad esempio ad un lato dell'ambiente. Supponendo che tale valore sia ad
es. 3.5 cm, si ricava il suo valore reale moltiplicando tale lunghezza
per il rapporto di scala. Così si avrà il valore 3.5 cm x
100 = 350 cm. che è il valore metrico reale del lato analizzato.
Per la determinazione dei valori angolari si procede graficamente utilizzando il goniometro, oppure se si procede per via analitica si misurano i tre lati di un triangolo costruito con due lati paralleli alle semirette formanti líangolo da misurare ed applicando un semplice calcolo matematico si risale al valore angolare. |
|||||||||||||||||||||||||
| a - Pianta
senza indicazioni di una scala numerica dove si può risalire ad
informazioni metriche assegnando un valore alle pedate della scala..
b - Determinazione dellíangolo formato da due pareti attraverso líapplicazione del metodo della trilaterazione. |
 
|
|||||||||||||||||||||||||
| Da supporto parametrato | Per ovviare ad i problemi connessi alle deformazioni
dei supporti sui quali sono eseguiti i grafici architettonici si eseguono
le cosiddette parametrature, cioè si traccia ai margini dei fogli
un riquadro (spesso é sufficiente solo su due lati) sul quale si
riportano le tacche delle misure utilizzate. Questa parametratura può
essere tracciata secondo valori regolari ma indipendenti dal disegno, ed
in questo caso possono essere utilizzati solo per valutare le possibili
deformazioni del supporto. Risulta conveniente, nel tracciare le tacche
di riferimento, eseguire la parametratura rispettando la scala del disegno
(fig. _). La parametratura eseguita quale riquadro consente di non tracciare
alcuna linea che vada a sovrapporsi al grafico e che quindi possa far commettere
errori di interpretazione nella lettura del grafico confondendo linee della
parametratura con linee del disegno. Accettando questo inconveniente, ovvero
annullandolo utilizzando linee di colore differente, si può tracciare
una griglia consentendo di poter poi correggere errori di deformazione
localizzati e non interessanti líintero grafico. Un esempio del primo tipo
di deformazione é quello che viene fuori da una riproduzione tramite
fotocopiatrice che potrebbe riprodurre il disegno non perfettamente al
100%, un caso del secondo tipo è quello che accade ad esempio lasciando
cadere dellíacqua sulla carta, dove viene a deformarsi solo intorno al
punto di caduta ed espansione dellíacqua. Ricordiamo che lo stesso calore
emesso dalle nostre mani é in grado di deformare la carta da schizzi
e ciò accade facilmente quando si lavora nelle giornate estive.
La carta assorbe facilmente líumidità presente nellíaria. Non entriamo
in merito ai vari tipi di supporto (carta normale, da schizzi e lucida,
poliestere, ecc.) ed alle loro capacità di resistere alle sollecitazioni
meccaniche e termiche.
|
|||||||||||||||||||||||||
| Vari tipi di parametratura: a) su due lati (riferita direttamente alla scala di riduzione), b) con tacche su tutti i lati, c) con griglia sovrapposta (spesso nel rilevamento archeologico tale griglia corrisponde alla maglia realizzata in campagna). | 
|
|||||||||||||||||||||||||
| Determinazione delle coordinate originarie di un punto rappresentato su una carta parametrata | Si supponga di voler conoscere la posizione di un punto A appartenente ad un grafico da cui desumere le informazioni riquadrato da una parametratura con tacche indicanti le misure di riferimento relativamente ad un sistema di riferimento cartesiano rappresentato dallíorigine indicata nei segmenti parametrati posti ai margini del foglio (Fig. 2). Si considera il grafico come composto da tanti settori quadrangolari realizzati tracciando le congiungenti i punti aventi le stesse coordinate e le stesse ascisse della parametratura. Si ottengono così dei poligoni quadrangolari che in assenza di deformazione risulterebbero rettangolari. Individuato il poligono che contiene il punto A, si leggono le coordinate del vertice più vicino allíorigine, quindi si riporta il punto A sui lati del quadrangolo. Il valore della variazione della lunghezza *L é data dalla differenza tra la misura originaria L' indicata numericamente sul grafico e quella L letta dal grafico: *L=L'-L. La variazione di lunghezza per unità di misura (variazione unitaria) è data da VL=*L/L. Il valore riferito alle coordinate ortogonali diviene: Ux=*x/x e Uy=*y/y. Quindi si leggono graficamente i valori delle coordinate del punto A riferite al sistema locale e si correggono dei fattori Ux e Uy. | |||||||||||||||||||||||||
| Ricerca della lunghezza originaria x del segmentoBC su carta parametrata |
  |
|||||||||||||||||||||||||
| Determinazione della lunghezza originaria di un segmento rappresentato su una carta parametrata | Per determinare la lunghezza di un segmento si può procedere in almeno due modi. Líuno è quello che si attua ripetendo per i due estremi del segmento líoperazione precedentemente illustrata per la determinazione delle loro coordinate. Si tratta quindi di calcolare la distanza in analiticamente (in nota la formula) o graficamente, accettando il fatto che la mappa abbia subito una deformazione omogenea cioè solo una variazione di scala. Con un righello si misura la lunghezza del segmento. Si determina il coefficiente di riduzione delle misure nella direzione del segmento dato. Si prolunga il segmento BC, sia da C che da B, nella direzione BC fino ad intercettare i lati del rettangolo rispettivamente nei punti E ed F. Rapportando la misura reale dei lati 14 e 34 alla corrispondente grandezza risultante dalla lettura sul grafico otteniamo la loro variazione di lunghezza. La variazione unitaria di lunghezza è così pari a U14=(14r-14g)/14r ed U34=(34r-34g)/34r. La lunghezza reale di un qualunque segmento sulla retta 34 sarà data da Xr=Xg*U34 da cui Xr=Xg*(34r-34g)/34r. Il coefficiente di variazione unitaria nella direzione BC sarà dato da Ubc=SQR((U34)*(U34)+(U14)*(U34)). La lunghezza originaria del segmento BC sarà dunque BCr=BCg*Ubc. | |||||||||||||||||||||||||
| Con l'uso dello scalimetro | Per leggere le misure sui disegni senza eseguire calcoli si usa lo scalimetro, ossia un righello che può essere piatto, riportante le graduazioni sui due lati, oppure a ventaglio o a forma di prisma a base rettangolare o triangolare) graduato sulle facce riportanti diverse scale di riduzione. | |||||||||||||||||||||||||
| a) uso dello scalimetro a sezione triangolare.
b) Tipi di scale metriche di riduzione riportate sugli scalimetri. |
 
|
|||||||||||||||||||||||||
| Immagini bidimensionali digitali | Utilizzando invece un mezzo informatico è possibile
digitalizzare una mappa per trasferire i dati dalla carta in computer.
Ove si debbano prelevare informazioni da una rappresentazione numerica, il valore della grandezza è automaticamente fornita dallíelaboratore. (Vedi anche digitizer e trattamento digitale - deformazione scanner). |
|||||||||||||||||||||||||
| Dalle mappe catastali | - omissis
|
|||||||||||||||||||||||||
| La scala Ticonica o trasversale | La scala Ticonica consente di determinare i sottomultipli
di una unità di misura riducendo le approssimazioni, ed è
quindi di ausilio nella esecuzione e nella lettura dei disegni in scala.
Essa viene costruita graficamente e consente di apprezzare i valori decimali
dell'unità di misura utilizzata, basandosi sul principio della similitudine
dei triangoli. La scala Ticonica si costruisce tracciando dieci rette -
numero dettato dal sistema di misurazione decimale utilizzato -, parallele
ed equidistanti. I segmenti più esterni vengono suddivisi in dieci
parti uguali. Si congiungono così i punti dei due segmenti detti
come in fig. 1, così da frazionare i restanti segmenti in unità
decimali. Questa costruzione può essere eseguita direttamente sul
segmento da misurare, o più agevolmente a parte su un foglio trasparente,
in modo da poterlo poi sovrapporre al segmento dato.
|
|||||||||||||||||||||||||
| Uso della scala Ticonica: misurazione di un segmento risultante 2,5 unità. |
 |
|||||||||||||||||||||||||
| Esemplificazione sullíutilizzo della scala Ticonica: misurazione della larghezza di un vano finestra. |
 |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
| IL RILEVAMENTO METRICO - GLI STRUMENTI PER IL RILIEVO DELLíARCHITETTURA | ||||||||||||||||||||||||||
| Viene quì di seguito proposta una sintesi degli
strumenti che vengono usualmente utilizzati per il rilevamento architettonico.
La selezione operata é stata dettata dalla necessità di offrire
essenzialmente un quadro generale di riferimento che desse la possibilità
di affrontare le problematiche connesse alla pratica attuativa del rilievo.
|
||||||||||||||||||||||||||
| La misurazione degli angoli | Per la determinazione di un punto di posizione incognita
nello spazio, è possibile servirsi della misurazione di grandezze
angolari. I tipi di gradazione usati nella misurazione degli angoli e riportati
sugli strumenti che si utilizzano per la loro determinazione sono: sessagesimale
in cui líangolo giro è suddiviso in 360 parti - gradi - , queste
a loro volta in 60 parti - primi - ed ancora in 60 parti - secondi. La
notazione utilizzata per indicarli é nn° nní nníí; centesimale
in cui líangolo giro è suddiviso in 400 parti - gradi -, queste
a loro volta in 100 parti - primi - ed ancora in 100 parti cioé
secondi. La notazione utilizzata per indicarli è nng nní nníí(a
volte viene anche utilizzato il sistema sessacentesimale in cui i gradi
dellíangolo sono indicati in gradi sessagesimali, mentre i primi ed i secondi
in centesimale, per cui assume la notazione nn°,nnnn); radiante in
cui allíangolo giro è assegnato il valore di 2? suddiviso in parti
frazionarie. La notazione utilizzata per indicarli è un valore frazionario
di ?. Tra le gradazioni indicate quella più usata è la centesimale;
con essa per esempio viene indicata la precisione degli strumenti attraverso
il valore minimo che essi consentono di apprezzare nella lettura.
Gli angoli sono ancora classificati a seconda del piano rispetto al quale sono riferiti. Nel piano orizzontale si classificano in azimutali, quando la direzione rispetto alla quale é posto lo zero del goniometro é il nord magnetico, e orientati, quando sono riferiti ad una direzione qualsiasi presa a base del rilievo. Gli angoli letti nel piano verticale passante per il punto in cui é indicato il punto base per il rilievo si classificano in zenitali, di inclinazione o di altezza, e nadirali, a seconda che lo zero della direzione di riferimento sia rispettivamente lo zenit, ossia la direzione verticale locale con origine verso la volta celeste (lo zenit), il nadir, ossia la direzione verticale locale con origine verso il nucleo del globo terrestre, ovvero la direzione orizzontale locale. Gli strumenti che permettono tali tipi di misurazioni sono denominati goniometri. Questi, tra i quali si ricordano il teodolite (o universale geodetico misuratore di angoli sia orizzontali che verticali) ed il tacheometro (strumento di minor precisione rispetto al precedente essendo le letture nellíordine dei primi centesimali), vengono utilizzati con la seguente modalità: posto lo strumento nel punto detto ìstazioneî, dopo aver letto (o assegnato) al cerchio graduato, posto nello strumento, il valore angolare di partenza, si collima il punto di cui si vuol conoscere la posizione riferita al punto stazione, dopo di ché si legge di nuovo il valore angolare riportato. La differenza dei due valori rilevati, utilizzando semplici formule matematiche, consente, in fase di restituzione, di risalire alla direzione rispetto alla posizione del punto base, sulla quale è posto il punto battuto. Spostando lo strumento in uníaltra stazione, collegata alla precedente, e procedendo in maniera analoga, ripetendo líosservazione al punto di posizione incognita, si acquisiscono le dimensioni dei tre angoli che ne permettono la determinazione univoca proprio del punto di posizione incognita. |
|||||||||||||||||||||||||
| La misurazione degli angoli - Strumenti | Goniometro
Archipendolo Bussola topografica Squadro Teodolite |
|||||||||||||||||||||||||
| La misurazione dei dislivelli | Nelle operazioni di rilevamento finalizzate allíinquadramento
del manufatto architettonico nel contesto è necessario individure
la posizione di un piano orizzontale al quale riferire tutti i punti che
discretizzano il manufatto. I punti saranno rappresentati con la loro quota
rispetto a tale piano (quota relativa) o relativamente ad altri piani secondari
riferiti a questíultimo. La distanza di un punto da un piano, misurata
nella direzione ortogonale al piano viene denominata quota del punto rispetto
al piano. Se il piano di riferimento è un piano orizzontale, allora
la quota è una distanza misurata secondo la direzione verticale.
La differenza di quota tra punti viene denominata dislivello. Per la determinazione
dei dislivelli si procede a misurare la quota dei singoli punti oppure,
tracciando un piano orizzontale rispetto al quale riferire la differenza
di quota (dislivello relativo). Per eseguire tale determinazioni sono utilizzati
strumenti semplici quali il LIVELLO AD ACQUA, o quei LIVELLI che fanno
uso di componenti ottici con líausilio di aste graduate. Oltre alla modalità
che prevedeno il riferimento ad un asse orizzontale, è possibile
utilizzare strumenti distanziometrici dotati di GONIOMETRO per la lettura
degli angoli e delle distanze, che attraverso la risoluzione dei triangoli,
forniscono, come risultato, la misura del dislivello ignoto.
|
|||||||||||||||||||||||||
| La misurazione dei dislivelli - Strumenti | Livello a cannocchiale
Livello ad acqua Livello da muratore |
|||||||||||||||||||||||||
| La misurazione delle distanze | In relazione alla strumentazione adoperata, si distinguono
differenti modalità operative di esecuzione e di controllo. Utilizzando
i distanziometri elettro-ottici che offrono la possibilità di una
lettura rapida ed automatica dei valori angolari e di distanza, e la memorizzazione
di un notevole numero di informazioni, si esegue un lavoro speditivo con
ottime tolleranze di precisione, con alti costi per le attrezzature e tempi
lunghi per la preparazione al rilievo. Servendosi invece di strumenti più
semplici, come la ROLLINA, líASTA METRICA, ecc., si annullano i tempi di
messa in stazione dello strumento elettro-ottico, si può lavorare
con molta più agilità nel rilievo del dettaglio, perdendo
nel contempo la possibilità di accumulare in memorie informatiche
i dati raccolti. Comunque venga eseguito un rilievo, le misure devono consentire
la definizione delle mutue posizioni degli elementi geometrici costituenti
líoggetto del rilievo, e quindi ogni controllo dello stesso che sarà
effettuato solo sulla base delle misure prese. Buona norma è quella
di prelevare le misure in andata e ritorno, cioé ripetendo la stessa
misurazione due volte invertendo la posizione del punto dal quale si parte
per eseguirla. A tal fine le metodologie e gli strumenti di rilievo utilizzati
dovranno garantire precisioni intrinseche: il valore dellíerrore commesso
non dovrà superare i limiti di accettabilità.
|
|||||||||||||||||||||||||
| La misurazione delle distanze - Strumenti | Asta graduata
Calibro Canna metrica Catena agrimensoria Distanziometri elettronici Metro Rollina metrica o fettucia metrica Stazione totale Tacheometro e stadia Triplometro |
|||||||||||||||||||||||||
| La segnalazione dei punti | Ai fini della individuazione dellíoggetto del rilievo
è necessario individuare una maglia di punti ai quali riferire le
misurazioni effettuate. Qualora sia possibile é preferibile che
la maglia di punti di inquadramento contenga líedificio da rilevare in
modo tale da relazionarlo al contorno ove si presume vi siano altri punti
di inquadramento in un contesto più ampio. Assume particolare importanza
la esecuzione di monografie dei punti principali, cioé grafie uniche,
riassuntive della posizione di punti - al fine di riconoscerne la posizione
reale sul terreno -, corredate eventualmente di misure e tali da costituire
una prima bozza di lavoro. Nei criteri di scelta dei suddetti punti bisogna
tenere conto di alcune considerazioni: essi devono essere univocamente
individuabili e conservare tale caratteristica almeno per tutta la
durata delle operazioni di rilievo; devono essere stabili, cioé
non devono mutare la loro posizione nel corso del tempo; devono essere
visibili almeno per terne in modo da consentire facili misurazioni e controlli.
Per ciò che riguarda la materializzazione stabile dei punti, questa può prevedere líuso di spigoli di fabbricato, di picchetti in legno, di picchetti in ferro, o di chiodi nel dettaglio; oppure può prevedere punti non stabilmente materializzati quali quelli che si individuano usando ad esempio le PALINE. Tralasciando la segnalazione dei punti vertici della rete a copertura del territorio, quali i vertici I.G.M. (CAPOSALDO) o i punti di controllo delle operazioni di Fotogrammetria aerea o terrestre, nel campo del rilievo architettonico di dettaglio può essere sufficiente evidenziare i punti che si andranno a rilevare - laddove sia possibile agire sulle superfici - con piccole croci, eseguite con gessetti o pitture (i colori da usare saranno il bianco ed il rosso per la loro efficacia visiva), con chiodi metallici crociati, ovvero, laddove si rischia di provocare danni allíoggetto del rilievo, con cartoncini, fili, ecc., adagiati o temporaneamente incollati sulle superfici. |
|||||||||||||||||||||||||
| La segnalazione dei punti - Strumenti | Caposaldo
Chiodo Gessetto Palina Vernice |
|||||||||||||||||||||||||
| Il tracciamento degli allineamenti | Quale ausilio ai lavori di rilevamento sono necessarie
una serie di operazioni preliminari che preparano alla vera e propria presa
di misura. Innanzi tutto bisogna scegliere una serie di punti ai
quali collegare líinsieme delle misure che saranno prelevate.
Questi, posti possibilmente lungo delle linee rette,- ALLINEAMENTI-, costituiscono
le basi dalle quali far partire le misurazioni successive . Quando si tratta
di tracciare allineamenti per distanze brevi, si può utilizzare,
ad esempio una lenza tesa tra due punti di appoggio. Se, invece, líinquadramento
del manufatto e delle sue parti nelle loro relazioni, (quali ad es. líingresso,
líandrone, il cortile, le scale) necessitano della costruzione di grandi
tracciati, si può far uso di allineatori e squadri con líutilizzo
di attrezzi quali le paline come ausilio alla costruzione della rete di
riferimento.
Allineamenti e assi di riferimento si possono generare con gli SQUADRI, ed in questo caso si assegna un valore angolare predefinito contenuto in una gamma abbastanza ristretta- ad esempio 30°, 45°, 90°, 0°/180°, Ö- , oppure con strumenti dotati di elevata precisione del cerchio graduato, come i TEODOLITI. Si parla ancora di allineamento anche quando si realizza una retta di riferimento rispetto alla quale prelevare i dislivelli tra punti: é questo il caso che prevede líutilizzo di LIVELLI per tracciare piani di riferimento. Ancora un allineamento verticale, utile per riferire il rilievo di cornici e di sporgenze ad una retta, si realizza con il FILO A PIOMBO che individua una linea di appoggio lungo un piano verticale. |
|||||||||||||||||||||||||
| Il tracciamento degli allineamenti - Strumenti | Allineatore Porro
Diottra Filo a piombo Lenza Livella Squadro |
|||||||||||||||||||||||||
| Il rilievo di sagome e profili | Quando oggetto dellíoperazione di rilievo sono forme
non discretizzabili in primitive geometriche elementari, ci si può
avvalere di strumenti che riproducono la loro forma su un supporto diverso.
Gli strumenti che discretizzano la forma in una serie di sezioni fatte
in posizioni e piani diversi sono: il PROFILOMETRO, costituito da una striscia
sottile di metallo (in genere piombo), che viene sagomata a formare il
profilo della forma indagata ed utilizzato soprattutto per il rilievo delle
cornici, il PETTINE costituito da una serie di aghi mobili, tenuti insieme
su un piano, a formare un pettine. Esso non fornisce dati metrici, ma restituisce
il profilo (sezione) dellíoggetto da rilevare, in modo da renderne possibile
la restituzione analogica. In particolari casi, il più delle volte
che trova applicazione nel rilievo archeologico, é la pratica che
prevede la riproduzione dellíoggetto tramite CALCHI (in gesso) per permettere
uníindagine più attenta per esempio rimandando líoperazione in un
laboratorio dove sono possibili tecniche che hanno bisogno di strumentazione
che non può essere trasportata sul luoghi del rilievo. Procedure:
ricalco, restituzione analogica, esecuzione calco in gesso, uso di un
cartoncino per riprodurre la sagoma.
|
|||||||||||||||||||||||||
| Il rilievo di sagome e profili - Strumenti | Profilometro
Pettine |
|||||||||||||||||||||||||
| Il controllo di spostamenti e deformazioni | Ai fini del collaudo dei manufatti architettonici, onde
accertarne la loro capacità di resistere alle sollecitazioni derivanti
dai carichi esistenti o di progetto cui sono sottoposte, sono indispensabili
operazioni di rilievo che richiedono particolare attenzione. In questo
caso sono indispensabili sia un alto grado di precisione degli strumenti
che una idonea preparazione tecnica degli operatori. Ciò che interessa
individuare è soprattutto come nel tempo la conformazione delle
masse architettoniche possa subire alterazioni: di conseguenza oggetto
di indagine sono gli spostamenti e le deformazioni.
Le procedure di rilievo, in questo caso, sono di due tipi: una prima, in cui il rilievo viene ripetuto in tempi diversi per consentire un controllo a posteriori delle strutture, ed una seconda in cui lo strumento rilevatore segue nel tempo il movimento dellíelemento da misurare. Uno strumento semplice del rpimo tipo è ad esempio una lente díingrandimento con un reticolo millesimale (in genere líequitacca è di 1/20 di mm corrispondente ad una tacca ogni 5 micron). Con questo strumento si stima la larghezza della lesione. Qui di seguito sono elencati alcuni degli strumenti che consentono sia la misurazione delle fessurazioni (fessurimetri) che delle deformazioni (Deformometri). Non sono indicati gli strumenti semplici di misurazione, quali líuso della matita con la quale si segna, datandoli, gli estremi di una fessura e che quindi dà una indicazione del movimento, il righello, il filo a piombo, ecc. che consentono, per questo specifico settore, misurazioni con approssimazioni elevate, quantunque offrano una prima possibilità di lettura dello stato di degrado in atto. |
|||||||||||||||||||||||||
| Il controllo di spostamenti e deformazioni - Strumenti | Le voci contenute in questo glossario sono tratte da
A. Alva, Rilevamento e diagnosi del quadro fessurativo, in «Recupero
Edilizio», pp. 205-206.
Calibro grafico - è in genere una mascherina o
una placchetta trasparente con riportati tagli o segni di diverso spessore.
Applicato sulla fessura dà la misura della larghezza. Non è
in grado di segnalare dati apprezzabili soprattutto se il movimento è
lento poiché rischia di percepirlo in tempi lunghi per fornire dati
di controllo significativi.
|
|||||||||||||||||||||||||
| Misurazione elettro-ottica delle distanze | Omissis
|
|||||||||||||||||||||||||
| Strumenti di misura ottici | Omissis
|
|||||||||||||||||||||||||
| Strumenti di misura elettro-ottici | Omissis
|
|||||||||||||||||||||||||
| Strumenti di misura elettronici | Omissis
|
|||||||||||||||||||||||||
| Nuove tecnologie per il rilievo: strumenti semplici per la misurazione elettronica delle distanze (EDM - electronic distance measuring) | I misuratori elettronici di distanza sono costruiti per
determinare la distanza tra due punti fissi. Essi utilizzano il principio
della trasmissione e riflessione delle onde elettromagnetiche nello spazio
cioé il metodo interferometrico nel quale viene emesso un raggio
modulato e viene poi misurato lo sfasamento del raggio di ritorno rispetto
a quello in uscita. Tali onde possono essere di tipo ultrasoniche per cui
non visibili, ovvero onde laser nel campo delle onde visibili. Il loro
funzionamento nelle linee generali è semplice: una sorgente posta
in A emette onde elettromagnetiche che giungono ad una stazione ricevente
situata in B; da questíultima esse vengono riflesse e rinviate in A. Qui
é posto lo strumento che misura líintervallo di tempo esistente
tra líemissione da A ed il ritorno in A dellíonda. Gli strumenti più
sofisticati di questo tipo permettono anche di fare elementari operazioni
matematiche - somme, sottrazioni, moltiplicazioni e divisioni - tali da
consentire sia di sommare o sottrarre misure parziali, o addirittura effettuare
in situ il calcolo delle superfici e volumi rilevati.
Essi possono essere composti esclusivamente da una trasmittente, o essere queste abbinate ad un apparecchio ricevente. La funzione della stazione trasmittente é quella di emettere un segnale elettromagnetico che riflesso dal punto oggetto di rilievo (o dalla stazione riflettente) torna alla stazione origine che grazie allo sfasamento dellíonda e tramite opportuni algoritmi restituisce il valore della distanza tra oggetto e punto stazione. Il valore rilevato potrà essere visualizzato su un display a cristalli liquidi (LCD) o memorizzato su memoria di massa per essere poi eventualmente trasferito in una stazione informatica. Tali strumenti, dotati di piccoli accumulatori che garantiscono una sufficiente autonomia di lavoro, sono facilmente trasportabili, consentendo così di effettuare numerose osservazioni per ogni singola campagna di rilievo. La distanza misurabile dipende dalla frequenza e dalla potenza del segnale emesso. I misuratori tascabili in genere arrivano - con solo stazione emittente - fino a 30 metri; se si utilizza anche una stazione riflettente - che non solo riflette, ma amplifica il segnale di ritorno si raggiungono distanze maggiori (fino a 100 metri c.a.) . Come si usa: Volendo determinare la distanza tra un punto A ed un punto B si posiziona la trasmittente nel punto A rivolgendo lo strumento in direzione del punto B. Se lo strumento emette esclusivamente uníonda elettromagnetica (nella banda degli ultrasuoni) non è possibile avere sufficiente certezza che il punto sul quale il raggio sonoro sarà riflesso è il punto B. La determinazione del punto B - viste le incertezze e il grado di approssimazione della misura - é possibile ricondurla alla determinazione di un qualunque punto appartenente ad un intorno ristretto del punto stesso. Se lo strumento è dotato di un mirino líoperazione descritta risulta di maggiore precisione. Se infine il raggio emesso é nello spettro dellíinfrarosso, il punto B da collimare sarà appunto colpito dal raggio tracciando un piccolo puntino rosso. Volendo determinare la distanza tra un punto A ed un punto B si posiziona la trasmittente nel punto A rivolgendo lo strumento in direzione del punto B. Premendo il pulsante che innesca líemissione del raggio elettro-magnetico avremo istantaneamente la lettura della distanza sul visualizzatore dello strumento. Alcuni strumenti ritardano la visualizzazione dei risultati in quanto effettuano più letture calcolando la misura presa quale media di queste. Le stesse modalità operative valgono anche quando vi sarà un apparecchio posto nel punto B in grado di riflettere il segnale trasmesso da A, essendo però necessario in questo caso predisporre líapparecchio in B posto su un supporto (ad es. un trepiede) o adoperato da un secondo operatore. Altri strumenti, molto più complessi dei precedenti vengono utilizzati per il rilevamento territoriale, ma alcune loro varianti grazie ad opportune modifiche si possono utilizzare al rilevamento architettonico. Tra questi ricordiamo il Radar (ad esempio i radar satellitari posizionati in modo da poter effettuare il controllo delle attività vulcaniche come quello che interessa il Vesuvio), il Tellurometro, lo scanner ad infrarossi, lo scanner multispettrale, il Sonar. |
|||||||||||||||||||||||||
| Termografia | Omissis
|
Parte quarta
Precedente - Successiva
Per proseguire clicca qui
|